Algorytmy uczenia maszynowego możemy rozpatrywać w dwóch kategoriach: metod uczenia bez nadzoru i z nadzorem. Między nimi jest bardzo istotna różnica.

A) Uczenie z nadzorem

Wyobraź sobie, że sprzedajesz samochody. Twój biznes rośnie, więc zatrudniasz kolejne osoby do pomocy, na przykład stażystów. Jednak masz problem: jeśli chodzi o Ciebie, to wystarczy, byś rzucił okiem na samochód – i już wiesz, ile mniej więcej jest on wart. Tymczasem Twoi nowi niedoświadczeni pracownicy tego nie potrafią.

Postanawiasz więc stworzyć program, który pomoże stażystom w wycenie wartości pojazdu. Aplikacja weźmie pod uwagę cenę podobnych pojazdów oraz cechy takie jak wiek pojazdu, marka i model czy wyposażenie.

Aby tego dokonać, zbierasz dane z minimum trzech miesięcy, rejestrując wszystkie informacje dotyczące sprzedaży pojazdów w okolicy. Przy każdej sprzedaży notujesz wiek pojazdu, markę i model, opis wyposażenia oraz – co najważniejsze – cenę, za którą pojazd został sprzedany:

Wiek	Wersja wyposażenia	Marka/Model	Cena sprzedaży
3	Komfort	Audi Q8	112200 zł
2	Standard	Mazda 6	47 000 zł
2	Średnia	Honda Civic	56 600 zł
1	Komfort	Citroen Cactus	53 000 zł
1	Komfort	Renault Megane	44100 zł

To dane uczące potrzebne do „treningu/uczenia”. Tak zebrane dane będą służyły do napisania aplikacji, która szacunkowo przybliży ceny innych pojazdów.

Wiek	Wersja wyposażenia	Marka/Model	Cena sprzedaży
5	Standard	Mazda 5	?

Dane zostaną użyte do uczenia przewidywania cen innych pojazdów. Takie uczenie nazywamy uczeniem z nadzorem. W tym przypadku w jego rezultacie otrzymujemy odpowiedź końcową, którą jest cena pojazdu. Aplikacja pozwoliła na wpisanie znanych danych pojazdów wraz z ich ceną – co umożliwiło poznanie logiki wyceniania tych pojazdów w odniesieniu do zebranych danych wejściowych.

Aby stworzyć program, musisz wpisać dane uczące do algorytmu uczenia maszynowego, który będzie próbował oszacować, jakie operacje matematyczne trzeba wykonać, by wyniki były satysfakcjonujące. W pewnym stopniu można to porównać do testu matematycznego, w którym symbole arytmetyczne zakryte, ale wyniki znamy.

By zbudować program, do algorytmu uczenia maszynowego musisz wpisać dane uczące. Algorytm ten próbuje oszacować, jakie operacje matematyczne trzeba wykonać, by otrzymać poprawne wyniki. Przypomina to trochę test matematyczny z wyczyszczonymi symbolami arytmetycznymi w działaniach, do których masz klucz odpowiedzi:

Tyle że symbole matematyczne zostały tu wymazane. Więc co dalej? Czy można odgadnąć, jakie działania pojawiły się w teście? Łatwo się domyślić, że trzeba „zrobić coś” z liczbami, które znajdują się po lewej stronie, aby uzyskać wynik znajdujący się po prawej. W uczeniu z nadzorem pozwalamy komputerowi samemu odgadnąć te relacje. W momencie gdy już dowiemy się, jakie działania były niezbędne, będziemy mogli rozwiązywać podobne zadania.

B) Uczenie bez nadzoru

Powróćmy teraz do przykładu ze sprzedażą pojazdów. Wyobraźmy sobie, co by się stało, gdyby sprzedawca nie znał ceny końcowej sprzedawanego pojazdu, a posiadał jedynie dane pojazdu jak np. marka, wiek czy wyposażenie? I tu właśnie pojawia się termin uczenia maszynowego bez nadzoru, gdzie algorytmy mogą dokonać wielu bardzo ciekawych operacji.

Wiek	Wersja wyposażenia	Marka/Model
3	Komfort	Audi Q8
2	Standard	Mazda 6
2	Średnia	Honda Civic
1	Komfort	Citroen Cactus
1	Komfort	Renault Megane

Uczenie maszynowe pozwala na odkrycie ciekawych rzeczy nawet wtedy, gdy nie będziesz próbował znaleźć nieznanej liczby (w tym przypadku ceny pojazdu).

Przypomina to sytuację, w której dostajesz od kogoś zapisane na kartce papieru liczby, a wręczający mówi: „Wiesz, nie mam zielonego pojęcia, co te liczby mogą oznaczać, ale może ty pomożesz mi rozwikłać tę zagadkę i sprawdzić, czy jest jakiś wzorzec albo zbiór danych?”

Jak możemy wykorzystać takie dane? Co możemy z nimi zrobić? Na początku możemy mieć algorytm, który automatycznie rozszyfruje z naszych danych dotyczących samochodów różne wymagania klientów. Może dowiesz się, że kupujący wybierają najczęściej dany model albo z danym wyposażeniem? Albo że młodsze auta mają lepsze wyposażenie? Znajomość oczekiwań klientów pomoże w ukierunkowaniu naszych działań marketingowych.

Innym ciekawym użyciem algorytmu byłoby automatyczne wykrywanie pojazdów o niezwykłych cechach. Być może dowiesz się, że te wyjątkowe samochody to jakieś rzadko spotykane modele? W takim przypadku możemy skoncentrować się na nich, angażując swoich najlepszych pracowników, którzy będą w stanie uzyskać lepszą cenę.

W dalszych wyjaśnieniach skupimy się na uczeniu maszynowym z nadzorem. Nie dlatego, że uczenie maszynowe bez nadzoru jest mniej interesujące czy użyteczne. Wręcz przeciwnie: jego znaczenie rośnie wraz z doskonaleniem algorytmów, gdyż umożliwia przetwarzanie danych bez konieczności oznaczania tych z prawidłowymi wynikami. Na marginesie: istnieje wiele innych typów algorytmów uczenia maszynowego, ale omówione do tej pory powinny na początek wystarczyć.

To wspaniale, ale czy przewidywanie ceny sprzedawanego pojazdu naprawdę uważa się za „uczenie” maszynowe?

Mózg człowieka jest w stanie przystosować się do większości sytuacji niej i nie potrzebuje do tego dokładnych instrukcji. Po jakimś czasie sprzedawania samochodów wyrobi sobie instynktowne przeczucie, „nosa” do właściwej wyceny na danym rynku, najlepszej strategii marketingowej, rodzaju klienta, którego dane auto może zainteresować itd. Celem badań nad sztuczną inteligencją (Artificial Intelligence, AI) jest właśnie możliwość powtórzenia takiego zachowania.

Istniejące dziś algorytmy uczenia maszynowego nie są jeszcze tak wszechstronne, jak ludzki mózg. Działają dobrze jedynie wtedy, gdy skupiają się na konkretnym zadaniu w ograniczonym polu. W naszym przypadku, by rozwiązać zadanie, które opiera się na przykładowych danych, zamiast definicji „uczenie” możemy użyć określenia „rozwiązywanie równań”. Dlatego takie uczenie określono mianem „uczenia maszynowego”.

Gdy za jakieś 50 lat odgrzebiemy ten artykuł, algorytmy silnej sztucznej inteligencji będą już istniały, a cały tekst wyda się mocno przestarzały. Kto wie, może nawet sztuczna inteligencja zrobi nam wtedy kanapkę?

Jak napisałbyś program, który szacowałby wycenę pojazdu tak, jak w powyższych przykładach?

Nie mając wiedzy o uczeniu maszynowym, zapewne będziesz próbował napisać jakieś proste reguły pomocne w oszacowaniu ceny pojazdu:

Jeśli będziesz pracować nad tym programem przez wiele godzin, to możesz stworzyć coś, co ma szansę działać. Jednak musisz wziąć pod uwagę fakt, że program nigdy nie będzie idealny i będzie miał problem z nadążeniem za wciąż zmieniającymi się cenami rynkowymi.

Czy więc nie byłoby prostsze, gdyby to komputer posiadał umiejętność wymyślenia za nas, w jaki sposób wykorzystać tę funkcję? Jeśli dostaniemy poprawny wynik, czyli jeśli ta funkcja wykona swoje zadanie, to jej dokładne działanie nas nie obchodzi. Nieprawdaż?

Jednym ze sposobów myślenia o tym zadaniu byłoby porównanie ceny pojazdu do pysznej potrawy jednogarnkowej, gdzie składnikami przysmaku byłyby wiek pojazdu, wyposażenie oraz marka i model to składniki „przysmaku”. Jeżeli jesteśmy w stanie oszacować, jak mocno każdy składnik wpływa na ostateczną cenę pojazdu, być może istnieją współczynniki proporcji poszczególnych składników, których wymieszanie zaowocuje określoną ceną końcową?

Podobne rozumowanie pozwoliłoby na redukcję funkcji do czegoś takiego:

Zwróćmy uwagę na pogrubione tajemnicze ciągi cyfry: .841231951398213, 1231.1231231, 2.3242341421 i 201.23432095. To są nasze przykładowe wagi. Jeśli odszyfrowalibyśmy idealne wagi, które działają dla każdego pojazdu, nasza funkcja mogłaby trafnie przewidywać ceny pojazdów!

Trywialny sposób, żeby znaleźć wagi, to wykonanie takiej procedury:

Krok 1:

Zacznij ze wszystkimi wagami ustawionymi na 1.0:

Krok 2:

Wykonaj funkcję dla każdego pojazdu, którego dane posiadasz, i zobacz, jak bardzo funkcja myli się w zgadywaniu właściwej ceny.

Użyj funkcji do oszacowania ceny każdego z pojazdów.
Na przykład, jeśli pierwszy został sprzedany za 250000 złotych, ale nasza funkcja odgadła 178 000 złotych, pomyłka wynosi 72 000 złotych dla tego jednego auta.

Teraz należy obliczyć kwadrat odchylenia od właściwej ceny dla każdego ze sprzedawanych aut. Powiedzmy, że w swoim zbiorze danych miałeś 500 sprzedanych samochodów i kwadrat odchylenia od ceny wzorcowej dla każdego z samochodów wynosił w sumie 82 123 373 złotych. To jest wskaźnik tego, jak „nieprawidłowo” nasza funkcja szacuje ceny samochodów.

Teraz weźmy końcową sumę wszystkich sprzedaży i podzielmy ją przez 500, aby uzyskać średnią tego, jaki błąd został popełniony dla indywidualnego pojazdu. Nazwijmy to średnim błędem cenowym naszej funkcji.

Jeśli będziemy potrafili zmniejszyć ten średni błąd cenowy do 0, modyfikując wagi, twoja funkcja będzie idealna. To by znaczyło, że w każdym przypadku nasza funkcja idealnie szacuje cenę pojazdu w oparciu o posiadane dane wejściowe. W takim przypadku cel został osiągnięty – średni błąd został obniżony tak bardzo, jak to tylko było możliwe, w odniesieniu do różnych wag.

Krok 3:

Powtarzamy krok 2 wielokrotnie, wybierając każdą możliwą kombinację wag. Jeżeli jakakolwiek kombinacja wag poprawia wynik (przybliża średni błąd do wartości 0) to staje się ona kolejną wyjściową kombinacją wag. Kiedy znajdziemy kombinację wag, które działają, problem jest rozwiązany!

A teraz czas na prawdziwe wyzwanie…
To proste, prawda? Pomyślmy, czego do tej pory dokonaliśmy. Wzięliśmy pewne dane, zostały one wpisane w trzy proste etapy, w efekcie czego otrzymaliśmy funkcję, która oszacuje cenę pojazdu o określonych parametrach.

Oto kilka faktów, które na prawdę Cię zadziwią: Badania w wielu dziedzinach (np. lingwistyka/tłumaczenia) na przestrzeni ostatnich 40 lat pokazały, że podstawowe algorytmy uczenia maszynowego potrafią wymieszać „potrawę”, wykonując swoje zadania nierzadko lepiej od ludzi tam, gdzie ludzie próbują znaleźć bezpośrednie i jawne zasady samodzielnie. Taki „bezmyślny” sposób uczenia maszynowego potrafi pokonać w tym zadaniu zwykłych ludzi, ale też ekspertów.

Końcowa funkcja jest naprawdę bezmyślna. Nie jest ona nawet w stanie wiedzieć, czym jest wyposażenie albo wiek pojazdu. Ona wie jedynie tyle, że wszystkie dane trzeba tak wymieszać, aby uzyskać poprawny wynik.

Prawdopodobne jest, że nie będziemy mieli najmniejszego pojęcia, dlaczego dana kombinacja wag w określonej funkcji działa poprawnie. Tak właśnie została napisana funkcja, której tak naprawdę nie rozumiemy. Możemy jednak pokazać, że działa ona całkiem poprawnie.

Wyobraźmy sobie, że zamiast selekcjonować parametry takie jak „wiek_pojazdu”, albo „marka”, nasza funkcja będzie sobie po prostu pobierała zbiór liczb. Powiedzmy, że każda liczba reprezentuje jasność pojedynczego piksela w zdjęciu zrobionym aparatem umieszczonym na dachu Twojego samochodu. Teraz powiedzmy, że zamiast wytworzyć odpowiedź na pytanie o „cenę”, funkcja będzie szacować wielkość nazwaną “liczba_stopni_do_skrętu_kierownicą”. Właśnie stworzyliśmy funkcję, która samodzielnie potrafi sterować naszym samochodem!
Trochę to dziwne, nieprawdaż? O co chodzi z tą „każdą możliwą kombinacją wag” w kroku 3? Tak naprawdę nie jesteśmy w stanie spróbować każdej kombinacji i wszystkich możliwych wag, aby znaleźć tą, która będzie pracować najlepiej. To by trwało wiecznie, bo liczby mogą być testowane w nieskończoność.

By tego uniknąć, matematycy wynaleźli wiele sprytnych sposobów szybkiego znajdywania dobrych wartości tych wag bez potrzeby testowania zbyt wielu. Oto jeden z tych sposobów:

Najpierw, napisz proste równanie, które reprezentuje krok 2.:

$$Koszt = {\sum_{i=1}^{500}( Przewidywania(i) – PrawdziwaOdpowiedź(i))^2\over 500 \cdot 2}$$

To jest nasza funkcja kosztu.
Teraz przepiszmy dokładnie to samo równanie, ale używając żargonu matematycznego uczenia maszynowego (na razie możesz to zignorować):

$$J(\Theta) = { 1 \over 2m } \sum_{i=1}^{m}(h_0(x^{(i)}) – y^{(i)})^2$$

Θ reprezentuje nasze bieżące wagi. J(Θ) oznacza ‘koszt dla naszych aktualnych wag’.
To równanie odzwierciedla, jak złe jest nasze szacowanie dla aktualnego zbioru wag.
Jeśli narysujemy tę funkcję kosztu dla wszystkich możliwych wartości wag dla parametrów „wiek_pojazdu” i „wyposażenie”, dostaniemy wykres wyglądający mniej więcej tak:

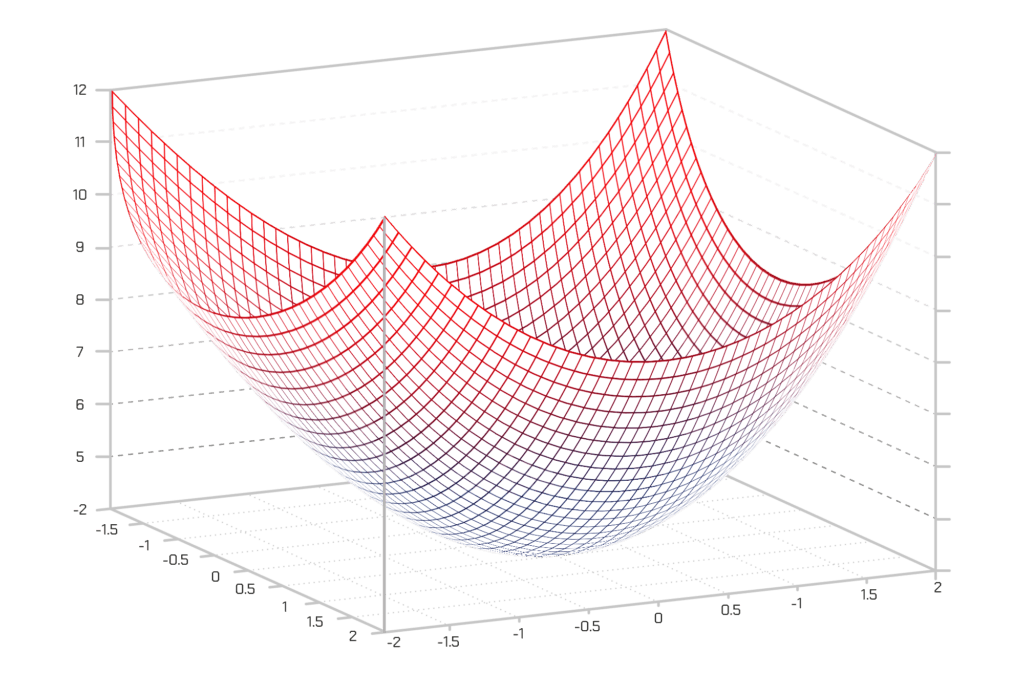
W tym wykresie najniższy punkt, zaznaczony na niebiesko, jest tym, dla którego nasz koszt jest najmniejszy – dlatego też nasza funkcja myli się tu najmniej. Najwyższy punkt jest tam, gdzie mylimy się najbardziej. W takim razie, jeśli możemy znaleźć wagi, które przenoszą nas w punkt najniższy, mamy naszą odpowiedź!

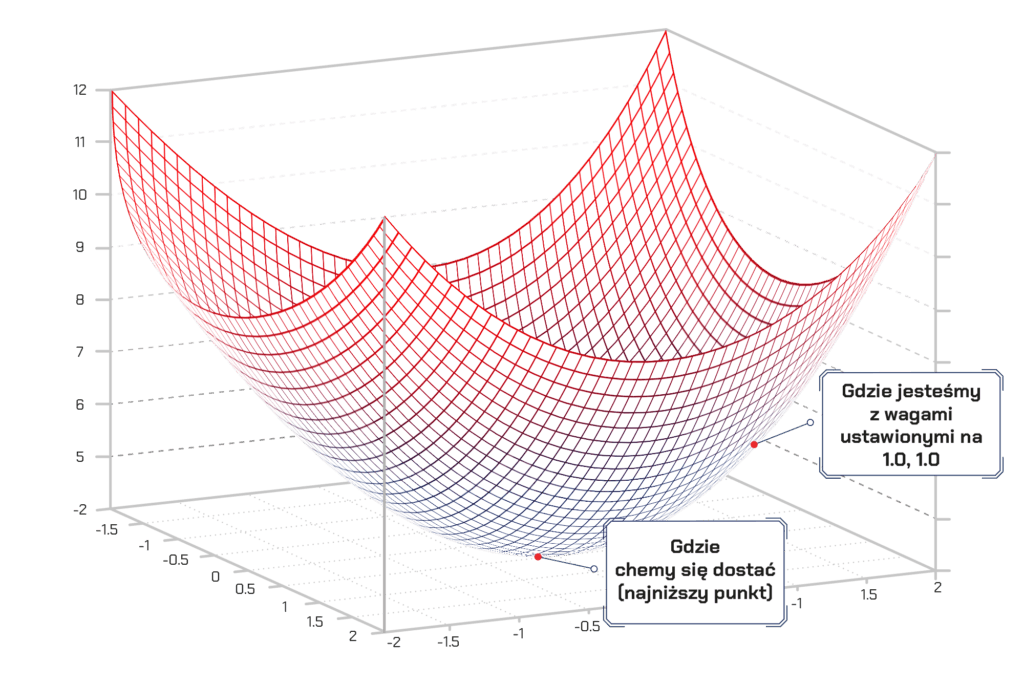
W takim wypadku koniecznie musimy jedynie zmodyfikować nasze wagi tak, abyśmy „szli w kierunku doliny”, czyli w kierunku niższych wartości na tym wykresie. Jeśli będziemy robić małe zmiany wag, które zawsze przenoszą nas niżej, dojdziemy tam bez potrzeby wykonywania zbyt wielu kroków. Jeżeli uczyliśmy się rachunku różniczkowego, wiemy, że pochodna z funkcji mówi o tym, jak jest ona nachylona w danym punkcie.

Parafrazując, mówi nam ona, w którym kierunku mamy iść, aby obniżyć wartość funkcji dla danego punktu z naszego wykresu. I tej wiedzy możemy użyć, by podążać w kierunku naszej doliny.

Dlatego jeśli policzymy pochodną cząstkową naszej funkcji kosztu względem każdej z naszych wag, możemy odjąć tę wartość od każdej wagi. W ten sposób zbliżymy się o krok w kierunku doliny, czyli ku minimum naszej funkcji. Robiąc to kilka razy – w końcu osiągniemy dno. A tam będziemy mieli kombinację najlepszych wag dla naszego problemu.

To podsumowanie jednego ze sposobów znalezienia najlepszej kombinacji wag dla naszej funkcji – metoda nazywana metodą gradientów prostych. Nie obawiajmy drążyć tematu, jeśli jesteśmy zainteresowani szczegółami.

Chociaż do uczenia maszynowego używamy bibliotek i właściwie problem jest rozwiązywany za nas, warto wiedzieć, co dzieje się „za kulisami”.

Co więc jeszcze jest ukrywane przez metody uczenia maszynowego, a co zostało ominięte?

Algorytm trójstopniowy, który został opisany powyżej, nazywany jest analizą wieloczynnikową regresji liniowej. Szacowane jest równanie liniowe, które zostaje dopasowywane tak, by prosta przechodziła przez wszystkie punkty z danymi. Potem to równanie jest używane do odgadnięcia ceny samochodów, których nigdy nie widzieliśmy na oczy, w oparciu o informacje, w którym miejscu pojawi się on na prostej. Takie równanie jest potężnym narzędziem, dzięki któremu mamy możliwość rozwiązania prawdziwych problemów.

Niestety przedstawione tu podejście może mieć swoje zastosowanie w prostych zagadnieniach, ale niekoniecznie będzie dobrze działało w dziedzinach bardziej złożonych. To dlatego, że ceny są zależnościami dość skomplikowanymi i nie zawsze ułożą się na ciągłej linii.

Jest jednak wiele sposobów na poradzenie sobie z bardziej zawiłymi problemami. Istnieje bardzo dużo innych algorytmów uczenia maszynowego, które dają radę z danymi nieliniowymi (sieci neuronowe czy metoda wektorów nośnych z tak zwanymi kernelami). Są też sposoby na użycie regresji liniowej w taki sposób, aby przybliżyć bardziej skomplikowane funkcje do naszych danych. W każdym jednak przypadku nadal celem jest ustalenie najlepszego zestawu wag.

W niniejszym artykule problem przeuczenia sieci został zignorowany. To dosyć proste: ukończyć algorytm z wagami, które zawsze pracują w sposób poprawny dla samochodów z naszego zbioru danych uczących, ale nie pracują poprawnie dla nowych samochodów, które nie były w oryginalnym zbiorze uczącym. Są sposoby, aby zapobiec takiemu zjawisku (regulacja, użycie testów walidacyjnych). W sprawnym posługiwaniu się narzędziami uczenia maszynowego umiejętność radzenia sobie z tym problemem jest kluczowa.

Konkludując, podstawowa idea jest bardzo prosta, jednak zabiera trochę czasu i doświadczenia, by zastosować uczenie maszynowe i uzyskać zadowalające rezultaty.

Kiedy zobaczymy, w jak prosty sposób uczenie maszynowe może zostać zastosowane do problemów prezentujących się jako naprawdę trudne (jak np. rozpoznawanie odręcznego pisma), możemy mieć wrażenie, że użycie uczenia maszynowego do rozwiązania dowolnego problemu to bułka z masłem. Wystarczy mieć tylko odpowiednią ilość danych, aby uzyskać odpowiedź.

Po prostu dostarczamy dane i patrzymy tylko, jak w magiczny sposób komputer rozpoznaje równanie, które dopasowuje się do danych. Trzeba jednak pamiętać, że uczenie maszynowe dobrze pracuje tylko dla tych problemów, które można rozwiązywać przy użyciu posiadanych przez nas danych.

Jeśli więc na przykład próbujemy znaleźć model, który przewidzi ceny pojazdów na podstawie płyt CD znajdujących się w schowku, to ta metoda raczej ma marne szanse powodzenia. Nie istnieje zwyczajnie żadna zależność pomiędzy płytami CD w schowku a ceną pojazdu. Dlatego nie jest ważne, jak mocne będą w tym przypadku próby. Po prostu komputer nie ma szans wydedukować żadnej relacji pomiędzy tymi danymi.

Z użyciem uczenia maszynowego możemy modelować jedynie zależności, które istnieją.

Warto zapamiętać, że jeśli człowiek (ekspert w swojej dziedzinie) ręcznie, przy użyciu dostarczonych my danych, nie podoła jakiemuś problemowi, to komputer tym bardziej sobie z tym nie poradzi. Natomiast algorytmy uczenia maszynowego mogą rozwiązać problem szybciej niż gdyby robił to człowiek.